Thierry Coilhac, juin 2022

Une nouvelle approche de la gravitation quantique basée sur l’hypothèse philosophique que “Seul ce qui est observable existe” .

Résumé

De notre postulat de départ que « seul ce qui est observable est réel » nous concluons que c’est l’interaction entre les particules élémentaires qui crée la réalité du monde. L’appartenance des objets macroscopiques à une même réalité nécessite que toutes les particules qui les composent, et donc en final toutes les particules de l’univers, interagissent deux à deux via une nouvelle interaction qui permet de confirmer leur existence mutuelle et définir la distance qui les sépare, laquelle est nécessaire pour définir la distance relative des objets macroscopiques auxquels elles appartiennent.

La cohérence maximum de l’univers, prenant en compte une vitesse de propagation de l’information limitée à C, est obtenue si deux particules interagissent tous les instants R/C où R est la distance qui les sépare. Leur interaction donne lieu à changement d’état correspondant à un quantum d’action ћ. Toute paire de particule effectue donc un changement de ћ tous les instants R/C.

Les caractéristiques d’un système à deux particules ainsi que le passage d’un repère relatif à un repère absolu conduisent à la loi de Newton à partir des considérations ci-dessus.

Le fait que la réalité du monde soit définie par l’interaction deux à deux de toutes les particules de l’univers s’applique à l’espace-temps et sa géométrie. Un élément de longueur n’est réel que s’il correspond à la distance définie par l’interaction de deux particules. Il en résulte que, comme en relativité générale, la matière-énergie définit la géométrie de l’espace-temps.

1. Une interaction entre particules pour entretenir la réalité

La question de savoir ce qui est réel ou non a toujours animé les débats tant philosophiques que scientifiques. Nous allons voir comment une réponse à cette question permet de conclure que la gravitation est une conséquence de la Relativité Restreinte (RR) et de la Mécanique Quantique (MQ).

Nous partons du principe très général que seul ce qui est observable est réel. Le terme « observable » doit être universel, tant pour l’observateur que pour l’observé. Il doit certes s’appliquer au chercheur observant des particules, mais ne peut nécessiter qu’un être humain doué de conscience observe l’objet considéré. Le mécanisme « d’observation » le plus général est l’interaction. Nous adoptons donc pour nouveau postulat que seul ce qui interagit est réel.

La question qui vient est alors est « qui interagit, mais avec quoi ? ». Avec quelque chose du monde réel. Ceci suggère que la notion de réalité est symétrique. Deux choses existent l’une pour l’autre si elles interagissent, elles appartiennent alors à la même réalité.

La question qui vient ensuite est « qui interagit, mais comment ? ». Toute interaction se fera en final au travers une particule élémentaire. De toutes façons un objet macroscopique n’a pas d’existence définie de façon précise, ce qui existe c’est l’ensemble des particules qui le composent. La notion de réalité se définit au niveau des particules élémentaires. La réalité du monde est définie par l’ensemble des particules qui interagissent. Ainsi ce qui permet à deux objets d’exister l’un pour l’autre, d’appartenir à la même réalité, c’est le fait que toutes les particules de l’un interagissent avec toutes les particules de l’autre.

Néanmoins, les interactions déjà connues seraient a priori insuffisantes pour entretenir la réalité des objets qui composent le monde. Nous sommes donc amenés à supposer qu’il existe une interaction entre particules qui entretient la notion de réalité. Nous l’appelons l’interaction O. Le fait que deux particules existent l’une pour l’autre se base sur leur interaction O.

2. Application à deux masses

Nous appliquons ce principe à deux objets de masses M1 et M2, et à deux particules P1 et P2 appartenant respectivement à M1 et M2. P1 et P2 sont séparées d’une distance R et supposées sans vitesse relative. P1 et P2 ont pour masse m1 et m2. Nous utiliserons la propriété énoncée par De Broglie « à chaque morceau d’énergie de masse propre m est lié un phénomène périodique de fréquence ν et que h ν = mc² ». Les ondes de De Broglie associées à P1 et P2 ont pour fréquence, nombre d’onde et longueur d’onde ν1, ν2, k1, k2, l1, l2. Pour chaque particule nous avons k = 2 π ν / C, où C est la constante universelle. La relation h ν = m C² conduit donc à k = m C / ћ, où ћ est la constante de Dirac ou constante de Planck réduite.

3. P1 et P2 interagissent tous les intervalles de temps R/C

L’interaction entre P1 et P2 s’accompagne nécessairement d’un changement d’état du système P1 – P2, et donc de chaque particule, lequel nécessite un échange d’information. Or selon la RR, l’information ne peut pas aller plus vite que C. Les deux particules ne peuvent donc pas interagir une fois puis une seconde fois immédiatement après. A partir de l’interaction et pendant un temps R/C aucune information venant de P2 ne peut arriver en P1. Elles ne pourront de nouveau interagir qu’au bout d’un temps R/C. Elles interagissent au plus tous les intervalles de temps R/C.

Lors de l’interaction, l’état de P2 vu de P1 est celui de P2 un intervalle de temps T=R/C plus tôt, T étant le temps qu’il faut à l’état de P2 pour arriver en P1. P1 et P2 interagissent avec un décalage dans le temps égal à R/C.

La distance D qui les sépare dans l’espace-temps au moment de l’interaction observée en P1 est donc telle que D² = C² T² – R² est nulle. L’interaction O est donc locale dans l’espace-temps dans lequel les particules sont séparées d’une distance nulle.

P1 et P2 interagissent-elles de nouveau dès que le temps R/C est écoulé ? Nous proposons une réponse affirmative qui permet au lien entre P1 et P2 résultant de cette interaction d’être le plus fréquent possible. Ce lien est même permanent mais avec un décalage dans le temps, puisqu’il n’existe alors pas dans le système à deux particules P1- P2 d’instant partagé entre P1 et P2 pendant lesquels elles n’interagissent pas. En effet, en dehors de ces instants d’interaction tous les R/C, P1 et P2 n’existent pas l’une pour l’autre puisqu’aucune information ne peut les relier.

4. L’interaction O entre P1 et P2 provoque leur rapprochement d’un quantum d’action

L’interaction entre P1 et P2 donne lieu à un changement d’état dont l’action A ne peut pas être inférieure à la constante de Dirac ћ conformément au principe énoncé par Niels Bohr. Nous considérons que cette action suit le principe de moindre action, c’est-à-dire qu’elle est la plus petite possible. Elle vaut donc A = ћ.

Rappelons que l’action A est le produit du déplacement par l’impulsion. Dans notre cas l’impulsion vaut ћ k. Nous n’utilisons pas l’impulsion définie comme le produit de la masse par la vitesse car nous considérons que les particules font un saut. Avant l’interaction les particules n’ont pas amorcé un mouvement en vue de l’interaction. C’est l’interaction qui provoque instantanément un changement d’état, la notion de vitesse n’est donc pas pertinente. D’où A = ћ k d, où d est un déplacement traduisant le changement d’état résultant de l’interaction. L’action A doit avoir cette valeur à la fois dans un repère associé à P1 et un repère associé à P2 car l’action est un invariant par transformation.

Nous évaluons ce déplacement vu de P1. La particule P1 ne peut percevoir ce déplacement qu’en constatant un changement de position de P2 par rapport à elle.

Nous nous plaçons tout d’abord en P2

Pour que le déplacement de P2 ait une action de valeur ћ elle doit effectuer un déplacement d2 tel que A = ћ k2 d2 soit égal à ћ. D’où d2 = 1/k2, ou encore d2 = l2/2 π , ou encore d2= ћ / m2 C. Dans le repère associé à P2, la nouvelle position de la particule P2 se trouve donc sur la sphère centrée sur son ancienne position et de rayon d2 = ћ / m2 C.

Plaçons-nous maintenant en P1

Remarquons d’abord que le système à deux particules P1 – P2 a une symétrie cylindrique, mais n’a pas assez de particules pour définir une variation angulaire. Pour l’illustrer notons que les deux configurations du schéma ci-dessous sont identiques.

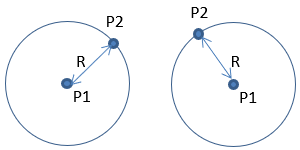
Première conséquence, un changement de position de P2 est toujours vu depuis P1 comme soit un rapprochement soit un éloignement. Nous privilégions l’hypothèse d’un rapprochement car si on considère que l’interaction doit maximiser la cohérence du système P1-P2, cet objectif sera atteint avec une réduction de la distance qui sépare les particules, ce qui augmentera la fréquence R/C à laquelle elles interfèrent.

Seconde conséquence, parmi toutes les nouvelles positions possibles de P2 vues de P2 nous devons éliminer celles qui ne sont pas sur l’axe P1 – P2 car vu de P1 elles aboutiront à un déplacement inférieur à d2 donc à une action inférieure à ћ. Dans le schéma ci-dessous, les nouvelles position P2’, P2’’ ne conviennent pas car la variation de distance vue de P1 valant d2 cos(θ) aboutit à une action ћ k2 d2 cos(θ) inférieure à ћ.

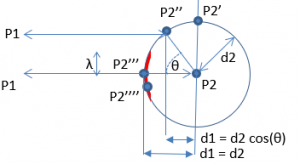
Néanmoins, la probabilité d’une position soit exactement sur l’axe est nulle car elle correspond à un point unique. Nous prenons en compte le fait qu’une distance n’est définie qu’à la longueur de Planck λ près. Toutes les positions possibles de P2 éloignées de l’axe P1-P2 d’une distance inférieure à λ sont considérées comme acceptables car donnent également lieu à une action valant ћ vu de P1. Les autres positions sont considérées comme impossibles, donc de probabilité nulle. En résumé, sur le schéma ci-dessus :

Toutes les positions sur la sphère de rayon d2 centrée sur P2, qui comme P’’’2 et P2’’’’ sont distantes de l’axe P1-P2 d’une valeur inférieure à λ sont considérées comme étant sur l’axe P1-P2, et correspondent donc à un déplacement de d2 mesuré dans R1. Ces positions occupent une surface π λ² qui est la surface du disque de rayon λ.
Toutes les autres positions sur la sphère de rayon d2 sont équivalentes à un déplacement d2 cos(θ) plus petit que d2 vu de P1, elles conduisent donc à une action inférieure au quantum d’action. Elles ont donc une probabilité nulle. On remarque que ce phénomène impose une conservation de la symétrie cylindrique autour de l’axe P1-P2 initial.

La particule P2 effectue donc un déplacement d2 avec une probabilité π λ²/ 2 π d2² (positions sur le disque de rayon λ sur la demi-sphère de rayon d2), et effectue un déplacement d2 avec la probabilité nulle (autres positions). Le déplacement moyen vaut donc d= d2 π λ²/ 2 π d2², c’est-à-dire d= λ²/2d2, ce que nous pouvons écrire sous les formes d=λ² k2/2, ou encore d = π λ² / l2 ou d = λ² m2 c / 2 ћ .

La distance d est le rapprochement de P2 observé par P1, c’est-à-dire le rapprochement de P1 dans un repère associé à P2. A chaque interaction, c’est-à-dire tous les instant R/C la particule P1 se déplace de la distance moyenne d = π λ² / l2vers la particule P2.

Remarque : Nous pouvons vérifier que la vitesse moyenne entre deux interactions est bien inférieure à C puisqu’elle vaut (π λ² / l2) / (R / C) , soit C x π λ² / l2 R. Cette vérification est nécessaire du fait que nous ayons pris ћ k comme valeur de l’impulsion.

5. Ce déplacement équivaut à une accélération gravitationnelle

Montrons maintenant que ce déplacement d’une distance constante d =π λ²/ l2 tous les intervalles de temps t = R/C est équivalent à une accélération et calculons la valeur de cette accélération. Pour cela voyons ce qui se passe sur plusieurs intervalles de temps successifs.

*) A l’instant 0, la particule P1 a une vitesse nulle dans le repère R1(0) qui lui est attaché. Au bout d’un intervalle t elle a parcouru une distance d et a acquis une vitesse v.

*) A l’instant t, dans le repère R1(t) qui lui est attaché et qui se déplace donc à la vitesse v par rapport à R1(0), elle a une vitesse nulle et est en situation de reproduire la même évolution que précédemment. Au bout d’un nouvel instant t, qui nous amène au temps 2 t, elle a de nouveau parcouru une distance d et a acquis une vitesse v. Donc dans le repère initial R1(0),

Elle a acquis la vitesse 2 v, correspondant à sa vitesse dans R1(t) à laquelle on ajoute la vitesse de R1(t) par rapport à R1(0).
Elle a effectué un nouveau déplacement de d + v t, c’est-à-dire son déplacement dans R1(t) auquel on ajoute le déplacement de R1(t) par rapport à R1(0).

*) A l’instant 2 t, dans le repère R1(2 t) qui lui est attaché et qui se déplace donc à la vitesse v par rapport à R1(t), elle a une vitesse nulle et est en situation de reproduire la même évolution que précédemment. Au bout d’un nouvel instant t, qui nous amène au temps 3 t, elle a de nouveau parcouru une distance d et a acquis une vitesse v. Donc dans le repère initial R1(0),

Elle a acquis la vitesse 3 v, correspondant à sa vitesse dans R1(2 t) à laquelle on ajoute la vitesse de R1(2 t) par rapport à R1(0).
Elle a effectué un nouveau déplacement de d + 2 v t, c’est-à-dire son déplacement dans R1(2t) auquel on ajoute le déplacement de R1(2 t) par rapport à R1(0).

*) Et ainsi de suite.

Au bout d’un temps T = n t, dans le repère initial R1(0)

La particule a acquis la vitesse V = n v.
Elle a parcouru la distance D égale à la somme des déplacements pendant tous les intervalles de temps t,

D = d + ( d + v t ) + (d + 2 v t) + …. + (d + (n-1) v t

D = n d + v t ( 1 + 2 + …. + (n-1))

D = n d + v t n (n-1)/2

La vitesse v est la vitesse finale de la particule après avoir parcouru une distance d en un temps t. En approximation, nous considérons que la distance d est égal à la vitesse moyenne vm multipliée par le temps, d = vm t, vm étant la moyenne entre la vitesse initiale nulle et la vitesse finale v et valant donc vm=v/2. D’où d = v t / 2, d’où v = 2 d / t

En utilisation les relation v = 2 d /t et n = T/t dans l’expression décrivant D nous obtenons

D = n d + (2 d / t) t n (n-1) / 2

D = n d + d n (n-1)

D = n² d

D = d T²/t² que nous mettons sous la forme
D = 2 ( ½ d/t²) T²

De même nous obtenons V = n v, V = n 2 d / t, V = 2 d T / t², V = 2 d/t² T

Au bout d’un temps T, la particule a parcouru la distance D = ½ ( 2 d/t²) T² , et elle a acquis la vitesse V = 2 d/t² T. Elle a donc subi une accélération de valeur g1 = 2 d / t²

Remarque : nous avons montré qu’un déplacement d’une distance constante à intervalles de temps constants dans le repère local est équivalent à une accélération constante dans un repère absolu. Le principe fondamental de la dynamique se démontre de la même façon.

Dans notre cas nous avons vu plus haut que d = λ² m2 C / 2 ћ et t = R/C.
L’accélération de la particule P1 vaut donc g1 = λ² m2 C / ћ x C²/R², ou encore g1 = λ² m2 C³/ ћ R²

En prenant en compte la relation λ² = G ћ / C³ où G est la constante gravitationnelle, nous avons
g1 = m2 G / R².

Le mouvement de la particule P1 observée dans son repère propre est donc identique au mouvement résultant de l’accélération gravitationnelle générée par la particule P2.

6. Attraction newtonienne entre les deux masses M1 et M2

Voyons maintenant qu’appliqué à toutes les particules qui les composent, ce phénomène conduit à l’attraction newtonienne des objets massiques M1 et M2.

Nous avons pris le cas d’une particule P1 de M1, et d’une particule de P2 de M2. Prenons maintenant en compte toutes les particules de M1 que nous notons P1i, i allant de 1 à N1 où N1 est le nombre de particules composants M1, et toutes les particules de M2 que nous notons P2j, j allant de 1 à N2 où N2 est le nombre de particules composants M2.

Chacune de particules P2j exercera sur chacune des particules P1i une attraction g1ij = m2j G / R²

Pour chacune des particules P1i toutes les accélérations g1ij s’additionnent, puisque P1i interagira avec chacune des particules P2j, provoquant à chaque fois un déplacement. L’accélération globale subie par P1i vaut donc :

g1i = (m21 + m22 .. + m2j … + m2N2) G / R², où m2j est la masse de la particule P2j

Or m21 + m22 .. + m2j … + m2N2 est la somme des masses de toutes les particules de M2, c’est donc la masse totale de M2. D’où g1i = M2 G / R², où g1i est l’attraction de M2 sur la particule P1.

Toutes les particules de P1i de M1 subissent la même accélération, donc M2 G / R² est également l’accélération de la masse M1 résultant de l’attraction gravitationnelle exercée par M2.

7. Ouvertures vers la Relativité générale

Notre postulat que « seul ce qui est observable existe » s’applique également à l’Espace-Temps. Un point de l’espace-temps n’existe que s’il est observable, ce qui nécessite qu’il puisse interagir et pour cela qu’il corresponde à la position d’une particule élémentaire.

De même une distance R de l’espace n’existe que si elle est observable, et donc si elle correspond à une distance séparant deux particules. Appelons P1 et P2 ces particules. En dehors des instants pendant lesquels P1 et P2 interagissent, P1 et P2 n’existent plus l’une pour l’autre car aucune information ne peut relier P1 à P2 comme abordé au paragraphe 3. La distance R n’existe donc que pendant les interactions entre P1 et P2, elle est définie par ces interactions. Ce raisonnement s’applique aux points et distances de l’espace, mais aussi de l’espace-temps.

Nous rejoignons ainsi le point de vue de la RG selon lequel l’espace-temps est défini par la matière-énergie, laquelle est composée des particules. Nous pouvons nous représenter l’espace-temps comme un scintillement de points, chaque scintillement correspondant à une particule en train d’interagir avec une autre. Seuls ces « flash » que sont ces scintillements existent dans l’espace-temps. Chaque flash s’accompagne d’une modification de la distance entre les deux particules qui interagissent pour aboutir à un changement d’un quantum d’action, et donc de la distance définie par ces deux particules, d’où la déformation de l’espace-temps par les particules, c’est-à-dire par la matière énergie.

On note que dans cette approche la densité de l’univers est nulle comme lorsqu’il était une singularité et que toutes les particules restent séparées par une distance nulle dans l’espace-temps.

8. Analyses

Notre approche fournit un mécanisme élémentaire à la gravitation. Celui-ci nous permet de formuler quelques commentaires relatifs aux constantes universelles et aux grandeurs physiques.

L’action est la grandeur fondamentale intervenant dans la gravitation. La gravité résulte du fait que l’interaction O entre deux particules provoque un changement dont l’action vaut un quantum d’action ћ. Les principes d’action minimum, de moindre action et de conservation de l’action par changement de repère jouent un rôle clé.
La constante C apparait dans un premier temps comme la vitesse à laquelle la réalité d’une particule arrive en une autre particule.
R/C représente le décalage dans le temps entre deux particules séparées par une distance R. Une particule voit l’autre particule telle qu’elle était un instant R/C plus tôt.
Sa mise au carré, à l’origine du terme R² dans la loi de Newton, résulte du passage d’un repère local à un repère absolu. Le terme 1/R² est donc doublement d’origine relativiste.
La constante C apparait ensuite dans l’impulsion des particules, laquelle intervient dans l’action relative au changement d’état suite à une interaction O. Le terme C³ que l‘on trouve dans G = λ² C³/ ћ est donc issu, pour un facteur C² du décalage dans le temps de deux particules interagissant, pour un facteur C de l’action associée au changement d’état.
Concernant la proportionnalité entre la masse et l’accélération gravitationnelle, la longueur d’onde l2 de l’onde de De Broglie associée à la particule P2, inversement proportionnelle à sa masse apparait à deux niveaux. Dans le paragraphe 4 :
- Quand on considère P2 seule, le résultat d2 = l2/ 2π reflète le fait que plus l2 est élevée, plus il y a aura une incertitude sur sa nouvelle position, donc plus forte sera la probabilité que sa nouvelle position soit éloignée de la position initiale. La longueur d’onde l2 apparait comme la quantification du déplacement moyen de P2. La masse m2, inversement proportionnelle à l2, apparait comme l’ancrage de la particule dans l’espace, sa résistance à un déplacement, ce qui rejoint la notion d’inertie.
- Quand on considère P2 dans le système P1-P2, le résultat d = π λ² / l2 reflète le fait que plus l2 est élevée, plus la probabilité est forte que la nouvelle position de P2 vue de P1 corresponde à une action inférieure au quantum d’action, et donc que le déplacement n’ait pas lieu puisque l’action ne peut être inférieure à ћ.
- On remarque que la valeur de l’action vue de la particule P1 fait passer le coefficient l2 du numérateur au dénominateur, car c’est cette fois une surface et non ne longueur qui intervient dans le calcul. De plus elle impose un déplacement sur l’axe P1-P2, donc une conservation de la symétrie
La longueur de Planck λ apparait comme la précision avec laquelle une longueur est définie, elle représente le grain de l’espace. Elle peut être considérée comme un quantum de distance. Plus sa valeur sera grande, plus l’attraction sera élevée car plus le nombre de positions finales possibles sur le disque de surface π λ² sera grand. Le terme λ² que l’on trouve dans G reflète cette surface.
La loi de newton s’exprime par l’équation g1 = λ² m2 C³/ ћ R². Elle ne passe pas par la notion de force qui n’est qu’un outil de calcul sans réalité physique. Ce qui est mesurable c’est un déplacement et non une force. Si le déplacement est rendu impossible du fait d’autres interactions, l’effet du mécanisme élémentaire à l’origine de la gravité portera sur un changement d’état d’une autre nature.

Concernant la Relativité Générale, une étude plus rigoureuse du mécanisme élémentaire proposé pourrait permettre d’aboutir à l’équation d’Einstein établissant une relation entre le tenseur métrique et le tenseur énergie-impulsion. Cela nécessiterait notamment la prise en compte dans une approche relativiste de la vitesse relative entre deux particules interagissant et sur le fait que la distance séparant les particules n’est pas R mais évolue avec le temps.

Ce mécanisme élémentaire ouvre des pistes pour expliquer les écarts entre la RG est les observations. La matière noire pourrait par exemple s’expliquer par le fait que dans certaines conditions l’interaction O donne lieu à un déplacement représentant plusieurs quantums d’action et non un seul, ou encore par le fait que notre mécanisme élémentaire ne n’applique pas qu’aux particules mais à tout « morceau de matière ». L’énergie sombre pourrait s’expliquer par le fait dans certaines conditions l’interaction O donne lieu à un éloignement et non plus un rapprochement pour lequel nous avons opté.

Ce mécanisme élémentaire permet d’imaginer des barrières gravitationnelles se basant sur un blocage de l’interaction O, ce qui ouvre des perspectives dans les moyens de transport.

Gravitation ontologique relativiste et quantique